[알고리즘] 깊이 우선 탐색(DFS, Depth First Search)

깊이 우선 탐색(DFS, Depth First Search)

DFS는 그래프에서 깊은 부분(자식들)을 우선적으로 탐색하는 방식이다. DFS는 스택이나 재귀 함수를 사용해서 구현할 수 있다. 탐색 과정이 한없이 진행되는 것을 막고 싶다면 깊이 제한(depth bound)를 사용해서 한업이 진행되는 탐색을 막을 수 있다.

 

• 장점
  
  • 현 경로상의 노드들만을 기억하면 되므로 저장공간의 수요가 비교적 적음
  • 최선의 경우, 가장 빠른 알고리즘. 운 좋게 항상 해에 도달하는 올바른 경로를 선택한다면, 깊이 우선 탐색이 최소 실행시간에 해를 찾음
  • 찾으려는 노드가 깊은 단계에 있다면 BFS보다 빠르게 찾을 수 있음
• 단점
  • 찾은 해가 최단 경로가 된다는 보장이 없음
  • 최악의 경우, 가능한 모든 경로를 탐험하고서야 해를 찾으므로, 해에 도달하는 데 가장 오랜 시간이 걸림

출처 : https://ko.wikipedia.org/wiki/%EA%B9%8A%EC%9D%B4_%EC%9A%B0%EC%84%A0_%ED%83%90%EC%83%89와 https://intrepidgeeks.com/tutorial/algorithm-basis-depth-first-search-dfs

 

 

 

파이썬 코드

DFS를 스택과 재귀로 구현한 방식의 결과는 각각 다르다. 스택을 활용한 경우 노드의 자식들을 스택에 추가한 후 맨 뒤에서 값을 꺼내서 해당 노드의 자식을 방문하고 ... 이런식으로 진행되어서 연결되어 있는 자식들의 마지막부터 방문하는 이런 느낌인데 재귀의 경우 노드의 자식 첫번째부터 재귀적으로 호출하기 때문에 자식들의 첫번째부터 방문한다.

 

 

그래프 데이터 예시

▶ 노드 정보가 숫자일 때

출처 : https://en.wikipedia.org/wiki/Depth-first_search

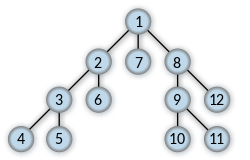
graph = [
    [],
    [2, 7, 8], [3, 6], [4, 5], [],
    [], [], [], [9, 12],
    [10, 11], [], [], []
]

# or

from collections import defaultdict

graph = defaultdict(list)
graph[1] = [2, 7, 8]
graph[2] = [3, 6]
graph[3] = [4, 5]
graph[8] = [9, 12]
graph[9] = [10, 11]

 

 

▶ 노드 정보가 문자일 때

출처 : https://zetawiki.com/wiki/%ED%8C%8C%EC%9D%BC:DFS_Graph.png

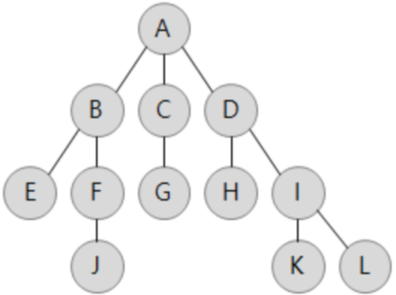
graph = {'A': ['B', 'C', 'D'],
         'B': ['A', 'E', 'F'],
         'C': ['A', 'G'],
         'D': ['A', 'H', 'I'],
         'E': ['B'],
         'F': ['B', 'J'],
         'G': ['C'],
         'H': ['D'],
         'I': ['D', 'K', 'L'],
         'J': ['F'],
         'K': ['I'],
         'L': ['I']}
         
# or

from collections import defaultdict

graph = defaultdict(list)
graph['A'] = ['B', 'C', 'D']
graph['B'] = ['E', 'F']
graph['C'] = ['G']
graph['D'] = ['H', 'I']
graph['F'] = ['J']
graph['I'] = ['K', 'L']

 

 

 

 

스택 활용

def dfs(graph, start):
    visited, stack = list(), list()
    stack.append(start)
    while stack:
        node = stack.pop()
        if node not in visited:
            visited.append(node)
            stack.extend(graph[node]) # 방문했든 안 했든 연결된 노드 모두 추가
    return visited

 

 

재귀 활용

def dfs(graph, v, visited, result):
    visited[v] = True
    result.append(v)

    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, visited, result)
    return result

 

 

아래는 방문 노드와 깊이까지 구하는 함수이다.

def dfs(graph, v, depth, visited, result):
    visited[v] = True
    result.append((v, depth))

    for i in graph[v]:
        if not visited[i]:
            dfs(graph, i, depth + 1, visited, result)
    return result

 

 

 

 

 

 

 

 

https://intrepidgeeks.com/tutorial/algorithm-basis-depth-first-search-dfs

[알고리즘기초] DFS(Depth-First-Search)

https://better-tomorrow.tistory.com/entry/DFS-BFS-%EC%9D%B4%ED%95%B4%ED%95%98%EA%B8%B0

DFS & BFS 이해하기 및 구현(C++)

https://ko.wikipedia.org/wiki/%EA%B9%8A%EC%9D%B4_%EC%9A%B0%EC%84%A0_%ED%83%90%EC%83%89

깊이 우선 탐색 - 위키백과, 우리 모두의 백과사전

https://wikidocs.net/123116

0.3.1 DFS와 BFS의 장단점