선형 회귀(Linear Regression)

머신러닝의 지도학습(Supervised Learing)에는 2가지 카테고리가 있다. 바로 분류(classification)와 회귀(regression)이다.

분류(classification)	회귀(regression)
분류에는 classifier(분류기)가 있다. 분류기에서 정답을 가진 data로 train을 해주고 난뒤, train이 끝나면, test시에는 정답이 없는 data를, 학습된 class를 기초로 판단하게 하는 것이다. classifier ex) knn, decision tree, SVM 등	사람의 무게를 줬을 때, 그 사람의 키를 예측하는 등의 문제

 

 

선형 회귀(Linear Regression)란?

변수 사이의 선형적인(=직선적인) 관계를 모델링 한 것이다. 즉, 선형 회귀란 주어진 데이터를 이용해 일차방정식을 수정해 나가는 것이다.

• 학습을 거쳐서 가장 합리적인 선을 찾아내는 것
• 학습을 많이 해도 완벽한 식을 찾아내지 못할 수 있음
• 하지만 실제 사례(ex.알파고)에서는 근사값을 찾는 것만으로도 충분할 때가 많음

 

 

 

아래의 두 직선 중 어느 직선이 더 예측하기 쉬울까?

많은 사람들이 왼쪽이 더 예측하기 쉬운 모델이라고 할 것이다. 왜냐하면 모든 점들이 직선상에 존재하기 때문이다. 이제 오른쪽 직선을 수치적으로 나타내보자!

오른쪽 직선

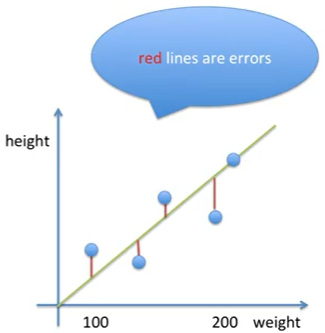
예측하기 위해 만든 모델인 y=ax+b직선과 실제 데이터를 찍어놓은 점들의 y값 차이를 error라고 한다. 즉, 아래와 같이 점과 직선 사이의 수직거리가 있어야 'error가 있다'라고 말할 수 있다. 그에 비해 왼쪽 직선의 경우 에러가 젼혀 없다. 그렇기 때문에, 왼쪽의 직선 모델이 에러가 전혀 없으므로, 왼쪽 직선모델이 더 낫다라고 할 수 있다.

 

cf) 참고

error	실제 데이터의 y값과 예측 직선 모델의 y값의 차이
square error	실제 데이터의 y값과 예측 직선 모델의 y값의 차이를 제곱해서 넓이로 보는 것

 

이제 수학적으로 더 파고 들어가 error이외에 square error로 한번 나타내보자!

square error는 error를 제곱해서 넓이로 보는 것인데 이렇게 하는 이유는 뭘까? 일단 우리 눈에 보이기 쉽고 수학적으로 볼 때, 에러가 조금이라도 있다면, 값이 증폭되어 큰 값과 작은 값의 비교를 쉽게 할 수 있다.

 

 

선형회귀에서 아래 두 직선 중에서 어떤 모델이 나은지 확인하려면 square error의 측면에서 확인해야 한다.

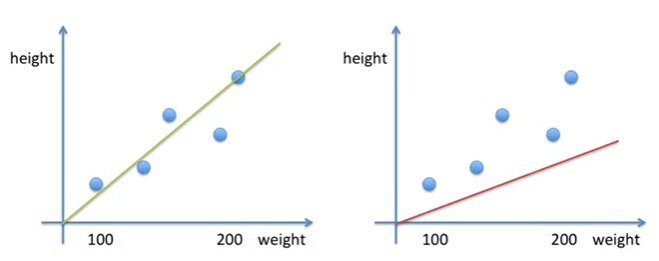
square error를 구하고, 그것을 평균 낸 Mean square error를 보면 왼쪽이 더 작다. 그러므로 왼쪽의 녹색의 예측 직선 모델이 예측을 더 잘할 것이다.

 

 

 

정답이 주어진 데이터가 있을 때, 가장 적합한 선(선형 회귀 모델)을 그으려면 어떻게 해야 할까?

즉, Linear Regression을 코딩하는 것이다.

여기서 사용하는 개념이 바로 Least Mean Square Error(LMS Error)이다. 아래의 공식을 사용한다.

Error는 예측값 h(x)(직선모델)에서 실제 값 y(실제 데이터의 y값)을 뺀 것이다. Square Error는 Error를 제곱한 값이다. Mean Square Error는 Square Error를 다 더해서 n으로 나누어 평균낸 값이다. 이 공식들을 사용해서 best한 직선(최적의 선형회귀모델)을 그을 것이다.

이 직선을 찾기 위해 Gradient Decent개념을 사용할 것이다. 그리고 이것을 사용하기 위해, 알아야 할 개념인 Cost function(=J(θ), 비용함수)이 Mean Square Error와 같은 것이라고 봐야 한다. 즉, 실제 값과 가설 값(예측값)의 차이를 제곱해서 평균낸 개념이 Cost function이다. 그리고 이 Cost function(=Mean Square Error)을 최저로 만드는 개념이 Least Mean Square Error이다. Least Mean Square Error는 Cost function을 최저로 만드는 목적을 가진 함수이므로 목적함수(Object function)이라고도 한다.

 

Gradient Descent

정답이 주어진 데이터가 있을 때, 최적의 선형회귀모델(직선)을 만들고, 그 모델의 Mean Square Error(=Cost function)을 최소로 만드는 최적의 직선을 찾아야 한다. 그 cost를 최소로 하는 직선을 구하는 과정을 학습(=train)이라 하고, 학습에 사용되는 알고리즘이 Gradient Descent 알고리즘이다.

 

최초의 직선을 h(x)=θx로 두고, 이것의 Mean Square Error(=1/n * Σ{(h(x)-y)^2},Cost function)을 최소로 하는 θ를 찾는 것이 목적이다.(머신러닝에서는 parameter들을 θ(세타)로 표현) 이제 Gradient Descent 알고리즘이 어떻게 사용되는지 알아보자.

1	Gradient Descent는 cost를 최소로 만드는 예측 직선인 h(x)=θx에서 최적의 θ을 업데이트 하면서 찾아내는 과정이다. 공식은 아래와 같다. (θ : 첫번째 θ로서, 맨첨에 초기화한 상수. Gradient를 태워서 cost를 최소로 만드는 θ로 점점 업데이트 될 것  α : learning rate로서, 학습 속도를 조절하는 상수.     : cost, Mean Square Error를 θ로 편미분 한 것) cf) θ와 α는 상수이므로 놔두고, cost를 편미분한 것을 통해 θ를 변화시켜 최적(cost를 최소화하는)의 θ로 업데이트 시킨다.
2	임으로 최초 θ는 1로, α는0.01로초기화 하고, θ에 대한 Mean Square Error를 시각화 해보면 아래와 같다. Gradient에서는 θ변화량이 (기존 θ)-(알파:양수)*(위의 왼쪽 그림의 θ=1일 때의 접선의 기울기:양수)으로 기존 θ에서 감소될 것 이다. 접선의 기울기가 나와있지 않지만 30이라고 가정하고 다음 θ를 구해보면 0.7(=1-0.01*30)이다. 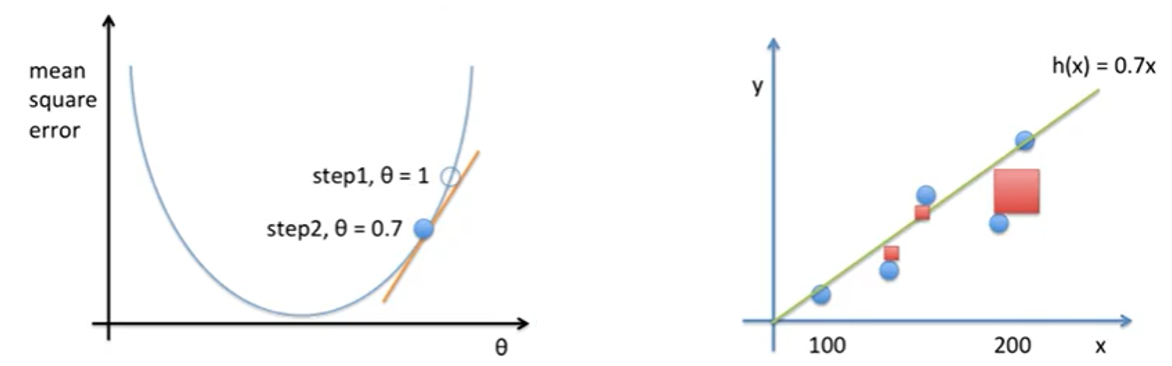cf) cost의 편미분을 구할 때에는,먼저 θ와 MeanSquareError에 대한 시각화 후, 접선의 기울기를 생각하는 것이 좋음 이제 업데이트된 θ에 대해서, Gradient를 통해 다음 θ를구해보자. Gradient에서는 θ변화량이 (기존 θ)-(알파:양수)*(위의 왼쪽 그림의 θ=0.7일 때의 접선의 기울기:양수)으로 기존 θ에서 감소될 것 이다. 접선의 기울기가 나와있지 않지만 5이라고 가정하고 다음 θ를 구해보면 0.65(=0.7-0.01*5)이다. θ의 값이 줄어드는 것을 확인할 수 있다.
3	Gradient의 θ업데이트 과정은 언제까지 반복될까? 2차 곡선상의 접선의 기울기(Mean Square Error)가 거의 0이 나오는 지점이 converage까지 반복해서 θ를 업데이트한다. θ를 Gradient를 통해 200번 업데이트를 해보자! Gradient를 통해 θ를 업데이트 하는 과정에서 1번째 h(x)(=1x, θ=1)와 200번째의 h(x)(=0.5x, θ=0.5)를 아래의 직선을 통해 비교해 보자! Gradient를 통해 200회 업데이트 된 θ로 구성된 직선이 Mean Square Error가 매우 작아진 것을 확인할 수 있다.

 

 

h(x)=θx+z가 주어졌을 때는 어떻게 풀 수 있을까?

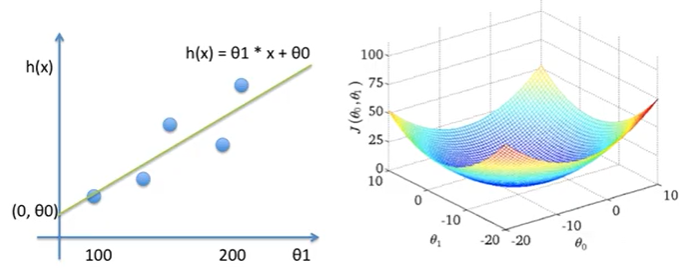
앞서 본 예제는 z가 0인 문제였다. 그러나 실제 상황에서는 z가 거의 붙어있다. 이럴 때는, θ를 θ1으로 z는 θ0으로 두고 h(x)=θ1x+θ0x 식을 사용해서 문제를 풀면된다.

앞서 본 예제는 Mean Square Error를 시각화 할 때는, θ가 1개뿐이라 2차 함수였다. 하지만 이제는 θ가 하나 더 늘어났으니 3차원으로 표시해야 한다.

 

 

Learning Rate(α)는 어떻게 설정할까?

Learning Rate는 θ가 업데이트되는 양을 상수로서 앞에 붙어서 조절한다. Learning Rate가 너무 작으면, 업데이트가 적게 되므로, θ들이 converage를 찾아서 내려가는 시간이 너무 오래 걸린다.

Learning Rate가 작을 때

 

반대로 Learning Rate가 너무 높으면, 급격한 업데이트로, θ가 converage를 지나쳐버리는 경우가 생긴다.

Learning Rate가 클 때

 

따라서, Learning Rate를 적절하게 설정해야 Cost(loss)가 수렴한다.

 

 

 

www.inflearn.com/course/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D%EC%9D%B4%EB%A1%A0-%ED%8C%8C%EC%9D%B4%EC%8D%AC%EC%8B%A4%EC%8A%B5/lecture/9538?tab=note

머신러닝 이론 및 파이썬 실습 - 인프런 | 학습 페이지