k-mean 클러스터링

k-mean 알고리즘은 비지도 학습(Unsupervised Learning) 알고리즘 중 하나이다.

 

cf) clustering(=군집,클러스터링)이란?

머신러닝에서 비지도 학습의 기법 중 하나이며, 데이터 셋에서 서로 유사한 관찰치들을 그룹으로 묶어 분류하여 몇 가지의 군집(cluster)를 찾아내는 것

 

 

k-mean 클러스터링이란?

k-mean 알고리즘은 굉장히 단순한 클러스터링 기법 중에 하나이다. 어떤 데이터 셋(set)이 있고 k개의 클러스터로 분류하겠다고 가정하면, 그 데이터 셋에는 k개의 중심(centroid)이 존재한다. 각 데이터들은 유클리디안 거리를 기반으로 가까운 중심에 할당되고, 같은 중심에 모인 데이터 그룹이 하나의 클러스터가 된다.

cf) mean이란? 각 클러스터의 중심과 데이터들의 평균 거리

 

 

k-mean 클러스터링의 STEP

1. 데이터를 준비한다.

 

2. 데이터에 대해 클러스터를 몇개 만들 것인지 결정한다.

• ex) 티셔츠 장사
  100명의 손님에게 모두 맞춤 티셔츠를 만들어 팔기 힘들다. 이 경우, 클러스터링을 통해 사이즈를 S, M, L 3가지로 평준화해서 팔 수 있다.

 

3. 클러스터링 할 때, 클러스터의 중심(centeroid)을 설정한다.

클러스터의 중심을 설정하는 방법은 아래의 3가지가 있다.

• randomly select centroid
• manually assign centroid
• kmean++

 

4. 클러스터의 중심에 대해, 모든 데이터 점(data point)들을 가장 가까운 클러스터 중심에 할당한다.

• 1번은 c1과 거리가 가장 가까움으로 빨간색으로 할당

• 2번도 c1과 거리가 가장 가까움으로 빨간색으로 할당

• 3번은 c2와 거리가 가장 가까움으로 초록색으로 할당

 

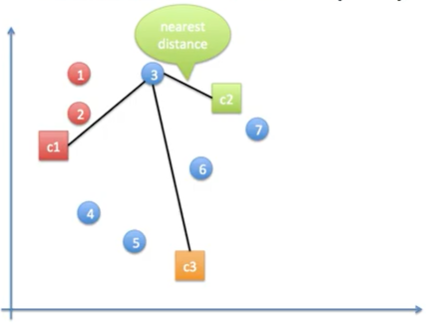
이러한 과정을 반복해서 아래와 같은 결과로 첫번째 iteration이 끝난다.

 

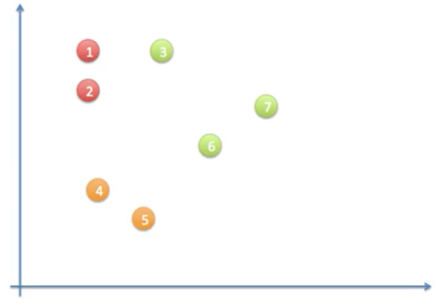
5. 각 클러스터의 중심을, 할당된 데이터 point들의 중심으로 옮긴다.

• 클러스터의 중심이 움직였다면, 다시 데이터들을 옮겨진 클러스터에 대해 가장 가까운데로 할당하는 과정이 반복된다.

 

6. 클러스터들의 변화가 없을 때까지 혹은 지정한 최대 횟수동안, 4번과 5번 STEP을 반복한다.

위의 상태에서 이제 두번째 iteration을 시작한다.

• 두번째 iteration시에, 데이터 point 4번은 c3와 가장 가깝기 때문에 새로운 클러스터인 c3에 할당되어 오렌지색으로 변경된다.

이러한 과정을 반복해서 아래와 같은 결과로 두번째 iteration이 끝난다.

 

이제 세번째 iteration을 위해 클러스터의 중심을 옮긴다.

 

세번째 iteration시에는 아무 데이터 point도 클러스터 할당이 변경되지 않았다. 그러면 클러스터의 중심도 더이상 이동하지 않게 된다.

 

 

 

클러스터의 중심(centroid)을 초기화하는 3가지 방법

randomly select centroid	랜덤으로 정하는 것
manually assign centroid	위도, 경도가 변수(속성, feature)일 때, 사람의 위치를, 3개의 도시(이미 정해져 있는 지점)를 클러스트의 중심으로 지정
kmean++	랜덤으로 클러스터 중심을 정했는데 결과가 만족스럽지 않거나 수동으로 줄 수 없는 상황에서 사용 kmean++ 알고리즘  1. 첫번째 데이터 point에 첫번째 클러스터 중심을 할당한다.(c1)  2. 첫번째 데이터에서 가장 먼 데이터 point에 두번째 클러스터 중심을 할당한다.(c2)  3. c1과 c2에 공통적으로 가장 먼 데이터 point에 세번째 클러스터 중심을 할당한다.(c3)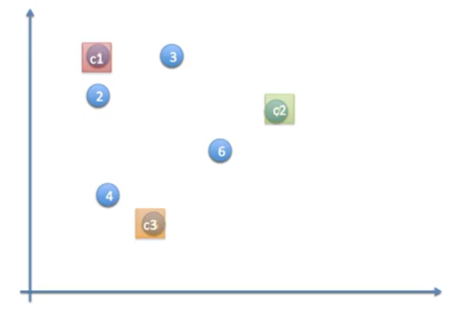

 

 

 

관련 실습

 

필요한 라이브러리

In [1]:

from sklearn.cluster import KMeans
import numpy as np
import pandas as pd
import seaborn as sb
import matplotlib.pyplot as plt
import random
%matplotlib inline

 

데이터 생성(30개 랜덤으로 생성)

In [2]:

df = pd.DataFrame( columns = ['x' , 'y'])

In [3]:

for i in range(30):
    df.loc[i]=[random.randrange(1,100),random.randrange(1,100)]

In [4]:

df

Out[4]:

	x	y
0	79	69
1	40	95
2	30	3
3	15	66
4	78	88
5	29	2
6	3	46
7	99	92
8	26	67
9	90	86
10	42	29
11	58	58
12	80	11
13	92	80
14	49	88
15	23	87
16	11	86
17	41	59
18	90	6
19	74	95
20	78	45
21	54	62
22	5	52
23	50	58
24	78	68
25	4	36
26	75	77
27	97	98
28	40	54
29	53	53

 

데이터를 그래프로 출력

In [5]:

# (x,y)좌표 형태로 30사이즈의 점으로 출력
sb.lmplot( x='x' , y='y', data=df, fit_reg=False, scatter_kws={"s":30}) 
plt.title('k-mean')
plt.xlabel('x')
plt.ylabel('y')

Out[5]:

Text(3.799999999999997, 0.5, 'y')

 

 

k-mean algorithm을 적용한 clustering(군집화)

In [6]:

# 데이터를 numpy 객체로 초기화
points=df.values

In [7]:

#데이터를 k-means알고리즘으로 3개의 cluster를 생성 ( 랜덤으로 생성)
kmeans=KMeans(n_clusters=3).fit(points)

In [8]:

#중심값을 생성
kmeans.cluster_centers_

Out[8]:

array([[54.2       , 10.2       ],
       [31.46666667, 64.46666667],
       [84.        , 79.8       ]])

In [9]:

# 데이터가 속한 클러스터
kmeans.labels_

Out[9]:

array([2, 1, 0, 1, 2, 0, 1, 2, 1, 2, 0, 1, 0, 2, 1, 1, 1, 1, 0, 2, 2, 1,
       1, 1, 2, 1, 2, 2, 1, 1], dtype=int32)

 

시각화

In [10]:

df['cluster'] = kmeans.labels_
df

Out[10]:

	x	y	cluster
0	79	69	2
1	40	95	1
2	30	3	0
3	15	66	1
4	78	88	2
5	29	2	0
6	3	46	1
7	99	92	2
8	26	67	1
9	90	86	2
10	42	29	0
11	58	58	1
12	80	11	0
13	92	80	2
14	49	88	1
15	23	87	1
16	11	86	1
17	41	59	1
18	90	6	0
19	74	95	2
20	78	45	2
21	54	62	1
22	5	52	1
23	50	58	1
24	78	68	2
25	4	36	1
26	75	77	2
27	97	98	2
28	40	54	1
29	53	53	1

In [11]:

# 위의 데이터를 시각화처리( seaborn 사용) - 각 클러스터별 다른 색으로 , 100 사이즈로 출력
sb.lmplot( x='x' , y='y', data=df, fit_reg=False, scatter_kws={"s":100},hue="cluster" )
plt.title('k-mean')

Out[11]:

Text(0.5, 1.0, 'k-mean')

 

 

 

 

m.blog.naver.com/PostView.nhn?blogId=eqfq1&logNo=221446499973&proxyReferer=https:%2F%2Fwww.google.com%2F

간단한 K-Means 알고리즘 실습

fenderist.tistory.com/85

[Tensorflow ] k-means 알고리즘 적용해보기

 

medium.com/@nsh235482/k-means-clustering-6ab85a2a32ad

K-means Clustering

bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-7-K-%ED%8F%89%EA%B7%A0-%EA%B5%B0%EC%A7%91%ED%99%94-K-means-Clustering

머신러닝 - 7. K-평균 클러스터링(K-means Clustering)

www.inflearn.com/course/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D%EC%9D%B4%EB%A1%A0-%ED%8C%8C%EC%9D%B4%EC%8D%AC%EC%8B%A4%EC%8A%B5/lecture/9538?tab=note

머신러닝 이론 및 파이썬 실습 - 인프런 | 학습 페이지