확률(Probability)의 정의, 규칙, 종류(결합, 주변)

확률(Probability)이란?

 - 우리가 얻는 임의의 표본은 모두 확률에 의한 사건

 - 사건이 일어날 가능성을 0과 1 사이의 실수로 표현한 것

 - 사건 : 발생 가능한 결과들의 집합, 표본공간의 부분 집합

 - 단순사건 : 발생 가능한 결과들 중 하나만 발생한 사건

 - 표본공간 : 일어날 수 있는 모든 가능한 단순사건을 모아 집합으로 표시한 것

• 모든 원소를 포함
• 상호 배반

 

 

표본공간

일어날 수 있는 모든 가능한 단순사건을 모아 집합으로 표시한 것

예시1) 동전을 1개 던지는 실험에 대한 표본공간 → {앞면, 뒷면}

예시2) 전구의 수명시간에 대한 표본공간 → { t | t ≥ 0, t : 실수 }

 

 

사건(event)

표본 공간 S의 임의의 부분집합

 

 

전통적 접근, 상대적 비율 접근, 주관적 접근으로 보는 확률의 정의

전통적 접근

 : 똑같은 가능성의 사건을 똑같은 확률값을 갖도록 정의

 ex) 주사위 확률, 동전 확률

 

상대적 비율 접근

 : 무수히 많이 시행하였을 때 그 사건이 일어난 비율이 수렴해가는 값을 그 사건이 일어날 확률로 정의

 ex) 주사위를 무수히 던졌을 때 5가 나온 비율

 

주관적 접근

 : 각자 생각하고 있는 어떤 사건이 일어날 가능성에 대한 믿음의 정도

 ex) 내일 비가 올 가능성

 

 

확률의 규칙

 - 표본 공간의 사건을 E1, E2, ... , En이라 할 때,

    ① 0 ≤ P(Ei) ≤ 1, for all i

    ② P(E1) + P(E2) + ... + P(En) = 1

 - 여집합 규칙

 - 합 규칙

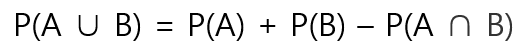
 - 상호배반 사건의 합 규칙 : P(A ∪ B) = P(A) + P(B)

   이 때, 상호배반 사건은 A∩B= ∅ or P(A ∩ B)=0

 

 - 독립사건 : 어느 사건이 다른 사건과 일어날 확률이 서로 무관할 때의 그 두 사건

   A, B가 독립사건이면 P(A ∩ B) = P(A)P(B), ---> P(A|B) = P(A) or P(B|A) = P(B)

 - 종속사건 : 독립사건이 아닌 경우

 

 - 곱셈 규칙

    P(A ∩ B) = P(B)P(A|B) or P(A ∩ B) = P(A)P(B|A)   →   A,B의 독립여부와 관계없이 항상 성립

 

 - 독립사건의 곱셈 규칙

    P(A ∩ B) = P(A)P(B)  →  A,B가 독립일때만 성립

 

 

확률의 종류

 - 결합확률 : 교집합의 확률

 - 주변확률 : 두 개의 변수를 동시에 고려하는 상황에서 어느 한쪽만을 생각할 때의 확률

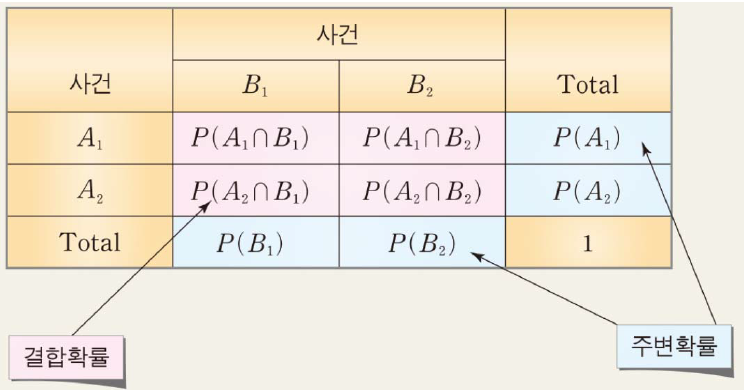
 - 조건부 확률 : 사건 B가 일어났다는 조건하에 사건 A가 발생할 확률

 

 

조건부 확률의 곱셈규칙

 

 

 

출처 : EXCEL, SPSS, R로 배우는 통계학입문/강상욱 외 8인 공저/자유아카데미/2014